Meshing or discretization in Computational Fluid Dynamics (CFD)
Computational Fluid dynamic is also known as CFD is a well-known method in the engineering field to solve fluid mechanics and heat transfer complex problems numerically with the aid of a computer which is tremendously advance nowadays. (Read Introduction to CFD here)
But, despite its advanced capabilities, the accuracy and validity of CFD compared to actual data is strongly dependent on its operator’s knowledge and skill, basically, it is just a calculator. The physics of fluid dynamic itself is very complex in nature and may have different approximation methods depend on its flow regime (viscosity, speed, density, laminar, turbulence, etc.) as well as its occurred phenomena (vorticity, adverse pressure gradient, etc.) hence, the parameters to be inputted will vary case by case. One important parameter to be considered is meshing or discretization. Meshing will strongly affect the quality of the resulted simulation, wether its accuracy, resolution or even its convergence characteristic. In general, the CFD engineer spent their time 70-80% of the whole simulation process to generate the right mesh. Before we go deeper into the selection of mesh type and more advanced topics, first we must understand what is meshing.
Meshing is a discretization process of continuous fluid domain converted into a discrete computational domain so that each part (also called an element) of its domain can be solved with the discrete equation. Then, why we should use a discrete equation instead of an analytical equation? This is because the nature of fluid mechanic’s governing equations consists of a non-linear partial differential equation, the Navier-stokes equation which is known as one of the unresolved yet mathematical problem.

To illustrate the discretization process, consider the area calculation below the curve above. If the curve is only a constant curve, we can simply calculate the area of the curve with length times height of the rectangle, or if the curve is only a linear curve then resulted picture is a triangle, we may simply calculate the area using 1/2*length*height of the triangle. But, what if the curve is a quadratic, cubic, polynomial, exponential or even an arbitrary curve? What we can do is to divide the area behind the curve into small section and calculates each section area then sum all of those area to “approximate” the total area below the curve (maybe you will ask, why not we use integral calculus? Yes, basically this is the idea of integral calculus, but the section length is infinitesimally small for integral calculus). The division process of the area is also known as meshing or discretization from the continuous curve into a discrete curve.
On the other hand, when we are about to calculate each section area, we use discrete area of each rectangle, the length times height equation, this is also known as equation discretization. In fluid dynamics, we often use the Finite Volume Method to discretize the Navier-Stokes equation, and basically these discretization methods are the core of CFD itself.
We can observe the characteristics of discretization from the area calculation case above. (1) we could get the more accurate result if we make the discretization even smaller, (2) not just accurate in term of its value, but also higher resolution graphically (smoother curve), (3) but, if the mesh is too small we also generate a lot of discrete equations to be solved, these equations need computational effort and time, so, make the mesh smaller is not straightforward solution to generate the optimum mesh.
Low-resolution mesh:

Let see the curves above, suppose the blue curve is an actual curve and we want to fit the blue curve with the orange curve which it’s resolution is constrained with the mesh (black lines). The orange curve not fits the blue curve well in the high-gradient region. This is the keyword, “high-gradient”, we should focus to refine the mesh in the high-gradient region so we can make a well-fitted graph without sacrificing a lot of computer effort and time. Following is the refined mesh in the high gradient region.
Refined mesh around the high-gradient region:

In Computational Fluid Dynamic (CFD) post-processing (or data interpretation), the resolution of its color also governed by the mesh size, it is analogous with your television or monitor resolution, higher the dot per inch, higher the resolution.
low-resolution mesh:

High-resolution mesh:
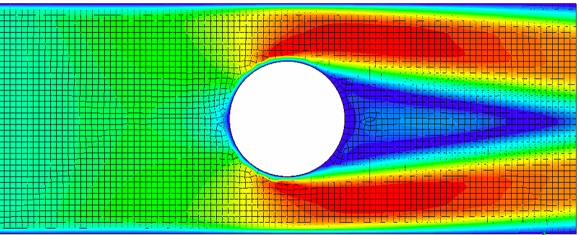
We will discuss more advanced topics about mesh in the next article, mesh types and mesh quality.
To read other articles, click here.

aeroengineering services is an online platform that provides engineering consulting with various solutions, from CAD drafting, animation, CFD, or FEA simulation which is the primary brand of CV. Markom.




Leave a Reply
Want to join the discussion?Feel free to contribute!