Momentum Analysis of fluid flow
In fluid mechanics, we are dealing with highly “squishy” material, unlike solid material which is easily modeled using relatively simple mathematical relationships. The nature of fluid flow complexity makes the “higher-order” mathematical modeling of fluid flow to get a detailed problem description such as the Navier-stokes equation by utilizing the differential equation approach or alternatively using the empirical method.
But, in engineering practice, sometimes we don’t even need a detailed problem description just to obtain some simple parameters. The simpler way to model this condition is by using the control volume method to estimate the result, in this case, momentum calculation.
Talk about momentum, the best way to describe it is by using the Newton’s law, mathematically described as:
F = m.a = d(m.v)/dt
With F = force, m = mass, a = acceleration, v = velocity, t = time. Then, the product of mass and velocity, m.v is also called linear momentum, hence the equation above can also be read as force is equal to the rate of change of linear momentum. Remember the force, velocity and momentum are vector quantity, so we must treat each equation for each direction (x,y,z).
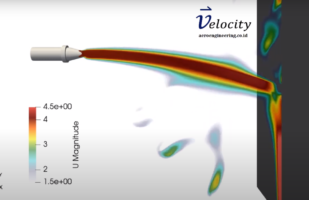
Back to fluid flow problem, consider water flow in a pipe then accelerated trough a hose then the water sprayed to the atmospheric condition. To calculate the reaction force generated by the momentum change of the water, first we must consider the control volume to focus our analysis:

To analyze the problem, we must define the general momentum law of fluid flow in the control volume (CV) as:
The sum of all external forces acting on a CV = The time rate of change of the linear momentum of the contents of the CV + The net flow rate of linear momentum out of the control surface by mass flow
With body force usually a gravity force and surface forces usually pressure, viscous and other forces. The first term of the right hand side of the equation is transient term, if the flow is steady (time independent), and the equation is simply become:
total F = total (B.mdot.v)out – total (B.mdot.v)in
with mdot = mass flow rate and B is the momentum-flux correction factor, with B = 1 for the case of uniform flow over an inlet and outlet. Back to our water hose problem, consider the mass flow rate of the water is 2 kg/s with flow enter the control volume (from the pipe) is 1 m/s, then accelerated after pass trough the reducing nozzle (read continuity) the speed become 5 m/s. Using the above equation, we can calculate the total F acting to the CV as (assume B = 1)
total F = 2*5 – 2*1 = 8 Newton
The total force is 8 Newton in the direction of outlet velocity (because positive result). In the outlet velocity direction? yes, right, we just calculated the action force, then the reaction force acted to the CV will be in the opposite direction (third Newton’s law).
This method is quite simple and fast compared to the differential analysis with a lot of simplification of course. We can also calculate more “complex” problem such as rocket reaction force or aircraft jet without any complex mathematical modelling for estimating the result.
To learn more about a more detailed fluid flow problem, you can read about the Navier-Stokes equation and Computational Fluid Dynamics (CFD) method for the numerical method to solve the complex differential equation by utilizing computer power.
To read other articles, click here.

aeroengineering.co.id is an online platform that provides engineering consulting with various solutions, from CAD drafting, animation, CFD, or FEA simulation which is the primary brand of CV. Markom.


Leave a Reply
Want to join the discussion?Feel free to contribute!