Teori dasar mekanika fluida: sebagai pengantar ke Computational Fluid Dynamics (CFD)
Selama berabad-abad, teori-teori mekanika fluida cukup sulit untuk diselesaikan secara analitis seperti mekanika benda padat, sehingga jalan yang paling mudah untuk memahami fenomena-fenomena aliran fluida adalah dengan eksperimen.
Namun, dengan berkembangnya teknologi komputasi menjadi memungkinkan bagi manusia untuk menyelesaikan persamaan-persamaan diskrit yang sangat kompleks menggunakan komputer dengan waktu yang masuk akal. Metode komputasi untuk menyelesaikan persamaan diskrit fluida itu sendiri kita kenal dengan Computational Fluid Dynamics atau CFD.
Seiring dengan perkembanganya, metode CFD mampu menangani berbagai macam kasus aliran fluida, mulai dari aliran incompressible seperti aliran pada sekitar mobil balap, aliran compressible seperti aliran pada sekitar jet supersonic, hingga aliran-aliran yang cukup kompleks seperti pembakaran, multifasa, interaksi dengan partikel dan lain sebagainya.
Untuk memodelkan aliran-aliran tersebut, seperti halnya teori fisika klasik secara umum, terdapat tiga persamaan atur (governing equations) yang mendefinisikan hukum kekekalan massa (kontinuitas), kekekalan momentum (persamaan Navier-stokes), dan kekekalan energi.
Persamaan atur (governing equations) mekanika fluida
Ada beberapa pendapat yang mendefinisikan ketiga persamaan atur fluida adalah persamaan Navier-stokes, namun Sebagian besar mendifinisikan bahwa persamaan Navier-Stokes hanyalah untuk persamaan momentum. Berikut penjelasan dari masing-masing persamaan atur mekanika fluida:
- Persamaan kekekalan massa (kontinuitas)
Persamaan kontinuitas dapat didefinisikan secara matematis sebagai berikut:

Persamaan 1.1 di atas merupakan persamaan umum dari hukum kekekalan massa yang berlaku untuk aliran kompresibel dan inkompresibel.
Dengan Sm adalah source term dari penambahan massa seperti misalkan untuk permodelan dispersi fasa kedua (contoh: evaporasi) atau sumber yang didefinisikan sesuai keinginan.
- Persamaan kekekalan momentum (Navier-Stokes)
Persamaan Navier-stokes secara umum didefinisikan sebagai berikut:

Dengan tau adalah tensor tegangan, sedangkan g, dan F berturut-turut adalah beban-beban gravitasi (dari dalam fluida itu sendiri) dan gaya eksternal seperti misalkan interaksi dengan disperse fasa lain atau porous media. Sedangkan tensor tegangan sendiri didefinisikan sebagai berikut:

Dengan miu adalah molecular viscosity, dan I adalah tensor unit.
- Aliran periodic
Sering kali dijumpai dalam permodelan aliran fluida seperti heat exchanger dengan jumlah tubes yang sangat banyak yang membuat geometri menjadi terlalu rumit untuk dimodelkan dan disimulasi karena membutuhkan effort komputasi (spesifikasi hardware, tenaga ahli, waktu, dan lain-lain) yang tinggi sehingga tidak feasible untuk dilakukan.
Dalam kondisi ini, jika fitur aliran bersifat berulang atau periodic seperti misalkan tube pada heat exchanger, maka kita dapat melakukan permodelan aliran periodic dalam CFD.
Secara umum, aliran periodic ini dibagi menjadi dua, yaitu (1) streamwise-periodic atau fully developed periodic; yaitu pola berulang yang searah dengan aliran yang menghasilkan pressure drop, dan (2) pola periodic yang tegak lurus terhadap aliran sehingga tidak menghasilkan pressure drop sepanjang arah pengulanganya.

Gambar 1.1. Contoh geometri periodic (sumber: ANSYS FLUENT Theory guide)
Gambar 1.1 di atas menunjukkan contoh geometri yang memiliki pola streamwise periodic.
- Aliran swirling dan rotating
Dalam aplikasi engineering secara umum, cukup banyak ditemui aliran yang bersifat swirling, misalkan aliran pencampuran bahan bakar dengan udara dalam suatu ruang bakar, mixing tank, dan lain sebagainya.
Permodelan CFD juga memungkinkan untuk memodelkan aliran-aliran tersebut dengan simplifikasi 2D dengan catatan aliran tersebut axisymmetry (simetri pada sumbu putar tertentu) seperti pada contoh Gambar 1.2. di bawah ini:

Gambar 1.2. Contoh aliran axisymmetry pada ruang bakar (sumber: ANSYS FLUENT Theory guide)
Berikut adalah bentuk persamaan momentum secara matematis untuk aliran swirling 2D:
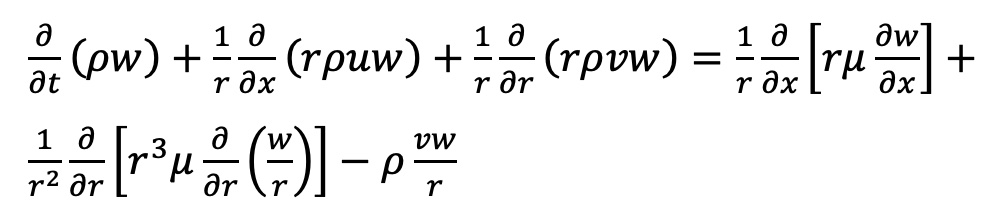
Untuk aliran dengan gradien tekanan kearah circumferential, permodelan 2D tidak dapat dilakukan. Adapun, tidak diperlukan prosedur khusus dalam pembuatan permodelan aliran 3D swirling.
- Aliran kompresibel
Untuk aliran fluida gas dengan kecepatan yang sangat tinggi, yaitu mendekati kecepatan suara, massa jenis gas yang awalnya dapat dianggap konstan dapat berubah karena tingginya perubahan tekanan yang terjadi. Adapun kecepatan suara dikarakterisasikan dengan bilangan mach, M yang didefinisikan sebagai berikut:

Dimana c adalah kecepatan suara gas, yang dapat dihitung dengan persamaan:

Dengan gamma adalah rasio dari specific heats (CP/CV).
Dalam permodelan CFD, anda hanya perlu mengaktifkan massa jenis fluida yang tidak konstan, misalkan menggunakan persamaan gas ideal atau persamaan gas real.
Untuk pemilihan solver pressure-based dan density based akan dibahas pada bab teori solver, namun pada intinya aliran kompresibel dapat diselesaikan oleh solver pressure-based maupun density-based.
- Aliran inviscid
Tidak ada fluida di dunia nyata yang benar-benar terbebas dari efek viskositas, namun dalam permodelan numerik CFD, “loncatan” dari permodelan inviscid menjadi viscous memiliki perbedaan effort komputasi yang sangat berbeda, karena model inviscid sangatlah sederhana secara matematis, sehingga membutuhkan waktu komputasi yang jauh lebih cepat.
Kasus-kasus yang dapat dimodelkan dengan inviscid adalah kasus dengan bilangan Reynold yang sangat tinggi, sehingga efek inersia dari aliran sangatlah dominan dibandingkan dengan gaya eksternalnya (gesekan), seperti contohnya aliran pada projectile atau pesawat dengan kecepatan tinggi.
Meskipun tidak dapat memprediksi secara akurat lift dan drag yang dihasilkan, namun dengan permodelan inviscid kita dapat dengan cepat melakukan trend analysis untuk menemukan desain yang paling optimal, kemudian setelah diperoleh desain tersebut, anda dapat menganalisisnya menggunakan model viscous untuk memperoleh data detailnya.
Secara sederhana, bentuk persamaan matematis dari persamaan inviscid untuk kontinuitas adalah sama dengan persamaan 1.1, kemudian untuk persamaan momentum adalah persamaan 1.2 dengan divergen dari stress tensor adalah 0, sedangkan persamaan kekekalan energi didefinisikan sebagi berikut:
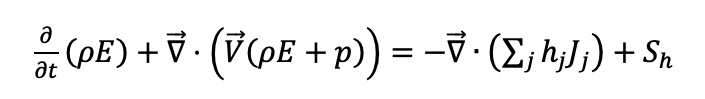
Dengan Sh adalah source term untuk energi. persamaan atur untuk aliran inviscid di atas dikenal juga dengan persamaan Euler.
>>BACA SELENGKAPNYA TEORI CFD DI SINI!
>>UNTUK ARTIKEL LAINYA TERKAIT CFD KLIK DI SINI!

aeroengineering services merupakan layanan dibawah CV. Markom dengan solusi terutama CFD/FEA.
Sumber: ANSYS FLUENT Theory guide



Leave a Reply
Want to join the discussion?Feel free to contribute!