Laminar and turbulent flow
Fluid mechanics is a very basic discipline in physics and engineering. Its usage is very broad and varied, from rocket and aircraft design, to biomedical analysis. Although it is years or even decades used and developed, but some of the formulation of fluid flow laws are still remain unsolvable, for instance the Navier-Stokes equations which is non-linear partial differential equation.
Unlike the common mechanics equations, for example Newton’s law, F = m.a, or energy, E = 1/2.m.v^2, the Navier-Stokes equations are not always can be solved exactly with existing mathematical tools. Even a million dollar price has been prepared to one who can solve this problem. One of the cause of this complexity is the nature of the flow which can be very random, unsteady, and chaotic which in turn make the equation “chaotic”, this condition also known as turbulent.
In definition, turbulent flow is a flow with random and chaotic pattern which contained eddies, swirls, and unsuitability within it. On the contrary, laminar flow is a streamlined pattern flow and predictable without any path disturbance. In the laminar flow, the Navier-stokes equations sometimes easy to be solved, for instance the Bernoulli equation, which is the form of Navier-Stokes equation for incompressible, inviscid, laminar, flow. Because of its complexity, even famous mathematician Richard Feynman said “turbulence is the most important and not-finished problem in the classical physics.
Because turbulent flow is quite hard to solve mathematically, some scientists prefer to use the experimental method to quantizes it, one of the most famous method is proposed by Osborne Reynold (1883), which is used non-dimensional ratio to predicts wether the flow is laminar or turbulent, this ratio also known as Reynold Number, Re = ratio between internal force to external force = rho*V*L/miu, with rho = fluid density, V = velocity, L = characteristic length (diameter for pipe, or chord for plate), and miu fluid viscosity.
Using this Reynold number, we can predict the laminar and turbulent flow quite accurate, for example, for flow in pipe, with Re = 0-2300, the flow is laminar, then for Re = 2300-4000 transition flow, and Re > 4000 is turbulent flow, no mater what is the fluid, or the pipe diameter, as long as the ratio within those ranges the flow will be known (laminar/turbulent). The physical meaning of this number is the higher the viscous force of the fluid (external flow), the flow will tend to be laminar, on the other hand, the higher the momentum (internal force) of the flow, the flow will be turbulent.
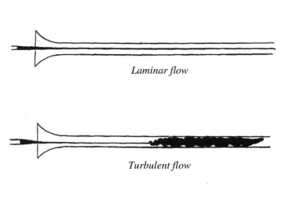

In the above illustration, the smoke plume is initially laminar, then moving upstream (increasing the distance, L), the local velocity also increasing because of the buoyant force, hence increasing the Re then finally the flow become turbulent.
Although we can predict wether the flow is laminar or turbulent, but to get more detail information about a certain flow pattern, we cannot do the same approach, for example for 3D flow we cannot find where are the locations of the turbulent occurs and how it affect in detail with the surrounding laminar flow. Instead of try to get the solution with detailed complete mathematical modeling, engineers prefer to “group” the specific eddies size and solve the equation for these “eddies flow” which make the problem much simpler; this method also known as turbulent modeling. The turbulent modeling is intensively used in the Computational Fluid Dynamics (CFD) simulation.
To read more topics about fluid mechanics or general engineering >> click here !



Leave a Reply
Want to join the discussion?Feel free to contribute!